Curiosidades - Tangram chino

El TANGRAM o juego de formas chino es un juego individual que estimula la creatividad. Con él se pueden construir infinidad de figuras.
En chino recibe el nombre de tabla de la sabiduría o tabla de los siete elementos. Como su nombre indica consta de siete figuras:
un cuadrado
un paralelogramo
cinco triángulos (dos grandes, dos pequeños y uno mediano).
Sus reglas son muy simples; con dichos elementos, ni uno más ni uno menos, se deben construir figuras. Además es un juego planimétrico, es decir, todas las figuras deben estar contenidas en un mismo plano.
 El tangram tiene gran importancia para el desarrollo del sentido espacial y para enriquecer la imaginación y la fantasía. Así mismo como ejercicio de concentración

Existen multitud de juegos basados en los mismos principios pero con distintas piezas. A casi todos estos rompecabezas se les conoce con el nombre de tangram. He aquí algunos de los más populares:

Tangram de 12 piezas

Tangram de 8 piezas



Tangram de 5 piezas

          

Tangram de Fletcher

Tangram pitagorico




Gabriela Tapia Romero  4to "A"  #33

El sorprendente poliedro de Császár

¿Qué es el poliedro de Császár?

El poliedro de Császár es un poliedro no convexo que no tiene diagonales (comparte esta propiedad con el tetraedro), es decir, cada uno de sus vértices está conectado con todos los demás por una arista. Podemos verlo en la siguiente imagen:

El poliedro de Császár tiene 7 vértices, 21 aristas y 14 caras triangulares. Por ello no cumple la fórmula de Euler:

Es topológicamente equivalente a un toro (esto es, una rosquilla) y su esqueleto es isomorfo al grafo completo .
Este poliedro fue descubierto por el topólogo húngaro Ákos Császár en 1949 y sirvió para resolver el siguiente problema:

Un toroide es un poliedro cuyas caras son todas polígonos simples (es decir, si fueran de plastilina podríamos deformarlas sin romperlas hasta obtener un disco) que además cumple que el propio poliedro es topológicamente equivalente a una esfera con uno o más agujeros que la atraviesan. ¿Es posible construir un toroide que no posea diagonales?

¿Cómo construir el poliedro de császár?

A la vista de la imagen anterior, el poliedro de Császár tiene una forma muy peculiar, extraña, hasta difícil de imaginar. Lo curioso es que es sencillo construirlo con papel a partir de estas dos plantillas:

Los pasos que debemos seguir para contruir el poliedro, según el gran Martin Gardner, con los siguientes:

• Recortamos las plantillas y coloreamos por los dos lados los triángulos sombreados. Después doblamos por las líneas de puntos para formar aristas “montañas” y por las líneas llenas para formar aristas “valle”.
• Para formar la base plegamos los dos triángulos más grandes hacia el centro y sujetamos con cinta adhesiva los vértices A uno junto al otro. Le damos la vuelta al papel y plegamos los triángulos más pequeños hacia el centro sujetando después con cinta las aristas B. Ya tenemos la base.
• La punta cónica de seis caras se forma pegando entre sí los lados C. Para colocarla sobre la base se unen los triángulos blancos con los triángulos sombreados y después se pegan cada uno de sus seis lados a los seis correspondientes de la base.

Hemos comentado antes que este poliedro no tiene diagonales y que el poliedro de Császár y el tetraedro son los únicos poliedros conocidos (con superficie acotada) que no tienen diagonales. Es sencillo comprobar que si un poliedro tiene vértices y agujeros, el hecho de que no posea diagonales obliga a que se cumpla la siguiente relación:

Teniendo en cuenta que los dos tienes que ser números enteros positivos y que además debe ser mayor que 3 (no hay poliedro con 3 o menos vértices), la solución con valores más pequeños es , que corresponde al tetraedro. Y la siguiente es , que es la que corresponde al poliedro de Császar. La siguiente solución posible es , que nos daría un poliedro con 44 caras y 66 lados, pero dicho poliedro no puede construirse. No se conoce ninguna solución más a partir de la cual se obtenga un poliedro que se pueda construir.

El dual de Császár

Dado un poliedro cualquiera, su poliedro dual puede construirse tomando un punto en cada una de las caras del poliedro inicial y uniendo el punto tomado en cada cara con los puntos tomados en las caras adyacentes a ésta. Por ejemplo, el poliedro dual del tetraedro es el propio tetraedro.

Si representamos el poliedro dual del poliedro de Császár aparece el denominado poliedro de Szilassi, descubierto por el matemático húngaro Lajos Szilassi en 1977. Este poliedro tiene el mismo número de aristas que el de Császár, 21, pero intercambia el número de caras con el número de vértices, esto es, tiene 14 vértices y 7 caras hexagonales. Aquí lo tenéis:

El poliedro de Szilassi y el tetraedro son los únicos poliedros en los que cada una de sus caras comparte una arista con el resto de caras del poliedro. Esta propiedad es la propiedad dual a la propiedad que comparten el tetraedro y el poliedro de Császár comentada al comienzo de este artículo.

Los dados de Rol

Los dados de rol utilizados en algunos juegos de rol tienen las formas de los sólidos platónicos: dado de veinte (D20), dado de doce (D12), dado de diez (D10), dado de ocho (D8), dado de seis (D6) y dado de cuatro (D4). Cada dado se utiliza para uno o más propósitos particulares dependiendo de cada juego. ademas se utilizan para hacer daños de elementos como: tierra:hexaedro icosaedro:agua dodecaedro:eter octaedro:aire tetraedro:fuego.

Algo de RM - EL PROBLEMA DE LOS 4 COLORES

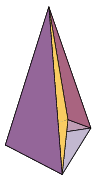
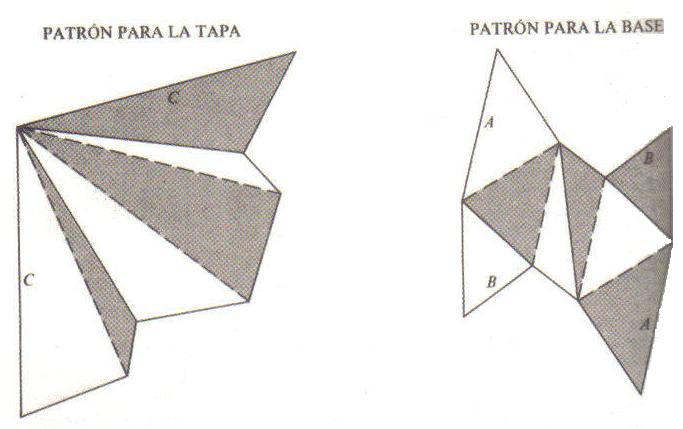
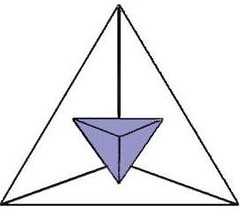
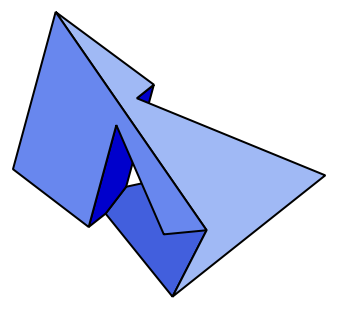
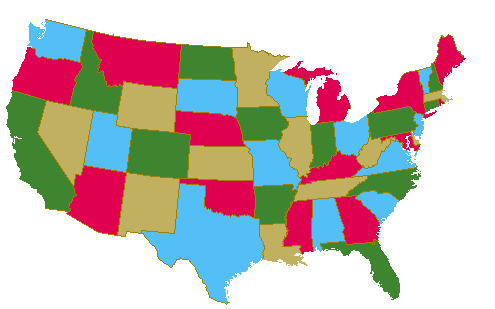"Bastan 4 colores para iluminar cualquier mapa de manera que no haya dos países vecinos del mismo color".   Ya los cartógrafos renacentistas lo sabían; sin embargo fue hasta 1850 que un estudiante inglés lo planteó como un problema matemático. En 1879 Alfred Kempe publicó la demostración en la revista Nature e ingresó a la "Royal Society", pero pocos años más tarde se le descubrieron errores. Casi 100 años después en 1976 dos norteamericanos lo demostraron usando una supercomputadora Cray que analizó todos los tipos de mapas durante 1,200 horas.  Pero muchos argumentaron que no era una demostración válida. En 1996 otros norteamericanos publicaron una demostración que hasta ahora nadie ha refutado.

Geometria En La Naturaleza

Pensamientos Matemáticos

"LA MEJOR FORMA DE LIBERARSE DE UN PROBLEMA ES RESOLVIÉNDOLO"

Brendan Francis

"LAS MATEMÁTICAS SON MÚSICA DE LA RAZÓN"

Silvester

"EL ESTUDIO PROFUNDO DE LA NATURALEZA ES LA FUENTE

MÁS FÉRTIL DE DESCUBRIMIENTOS MATEMÁTICOS" 

Joseph Fourier  

"LAS MATEMÁTICAS TIENEN INVENCIONES MUY SÚTILES Y QUE

 PUEDEN SERVIR DE MUCHO, TANTO PARA CONTENTAR

A LOS CURIOSOS COMO PARA FACILITAR

TODAS LAS ARTES Y DISMINUIR

EL TRABAJO DE LOS HOMBRES"

Descartes

"LAS MATEMÁTICAS SOSTIENEN LA ARMONÍA DEL MUNDO"

Albee

"LAS MATEMÁTICAS NO SOLAMENTE POSEEN LA VERDAD,

SINO LA SUPREMA BELLEZA, UNA BELLEZA FRÍA Y

AUSTERA, COMO LA DE LA ESCULTURA, SIN

ATRACTIVO PARA LA PARTE MÁS DÉBIL

DE NUESTRA NATURALEZA"

Bertrand Russell

"CÓMO ES POSIBLE QUE LA MATEMÁTICA, UN

PRODUCTO DEL PENSAMIENTO HUMANO

INDEPENDIENTE DE LA EXPERIENCIA,

SE ADAPTE TAN ADMIRABLEMENTE

A LOS OBJETOS DE LA REALIDAD"

Albert Einstein

"ASÍ ES, PUES, LA MATEMÁTICA: TE RECUERDA LA FORMA INVISIBLE DEL ALMA,

DA VIDA A SUS PROPIOS DESCUBRIMIENTOS, DESPIERTA LA MENTE

Y PURIFICA EL INTELECTO, ARROJA LUZ SOBRE NUESTRAS

IDEAS INTRÍNSECAS Y ANULA EL OLVIDO

Y LA IGNORANCIA"

Proclo

"LA GEOMETRÍA TIENE DOS GRANDES TESOROS:  UNO ES

EL TEOREMA DE PITÁGORAS, Y EL OTRO LA DIVISIÓN

DE UNA LÍNEA EN LA PROPORCIÓN DEL MEDIO Y

LOS EXTREMOS.  EL PRIMERO SE COMPARA

CON UNA MEDIDA DE ORO, Y EL

SEGUNDO CON UNA PIEDRA

PRECIOSA"

Johannes Kepler

Ilusiones ópticas con sólidos geométricos

El secreto del billar es la geometría

Si hay un deporte en el que los ángulos juegan un papel fundamental, ese es el billar. De hecho, para los grandes billaristas lo básico para practicarlo con éxito no es tener un buen golpe de muñeca, sino poseer unas nociones básicas de geometría para saber elegir qué golpe dar. Eso sí, no es el único deporte donde juega un papel importante. El estudio de los ángulos ha estado presente en la vida cotidiana del ser humano desde la antigüedad. Por ejemplo, los egipcios ya calculaban con precisión el ángulo de sus pirámides para garantizar la resistencia de sus paredes.



Leonhard Euler

Leonhard Euler fue uno de los más grandes genios de las Matemáticas. Pues bien, otra faceta de la que al propio Euler le gustaba hablar era la de calculista. Sus investigaciones en teoría de números se vieron apoyadas por el hecho de que dominaba mentalmente no sólo los 100 primeros números primos (1,3,5,7,11,13…), sino también sus cuadrados, cubos, cuartas, quintas y sextas potencias. Era capaz de hacer mentalmente difíciles cálculos, algunos de los cuales requerían retener en la cabeza hasta 50 cifras.


 

Definiciones Geométricas

Concepto:

·        Arista: Segmento donde se encuentran (intersección) dos caras de un sólido.

·        Vértice: Punto de intersección de dos o más lados (caras).

·        Bases: Son los lados inferiores de un sólido

·        Polígono: Figura cerrada formada por tres o más segmentos de recta.

·        Sólidos: Figuras del espacio que tienen tres dimensiones (largo, ancho, alto).

·        Prismas: Sólido con dos bases, las cuales son regiones poligonales y congruentes. Sus caras son figuras planas. 

·        Pirámide: Sólido con una sola base poligonal, cuyas caras son todas triangulares y se encuentran en un solo punto.

·        Cilindro: Sólido cuyas bases son dos círculos paralelos y congruentes.